Triply electronically excited (TREE) four-wave mixing is the electronic analogue of TRIVE, and most of the same concepts can be applied here.  Just as in TRIVE, signal is found at the phase matched direction $k_1 - k_2 + k_{2'}$ for output frequencies of $\omega_1 - \omega_2 + \omega_{2'}$, and the three laser interactions used can be used in any time ordering to provide resonant interactions with two fundamentals and a combination bands.  The key difference here is that the lasers are tuned to interact with electronic state manifolds. 

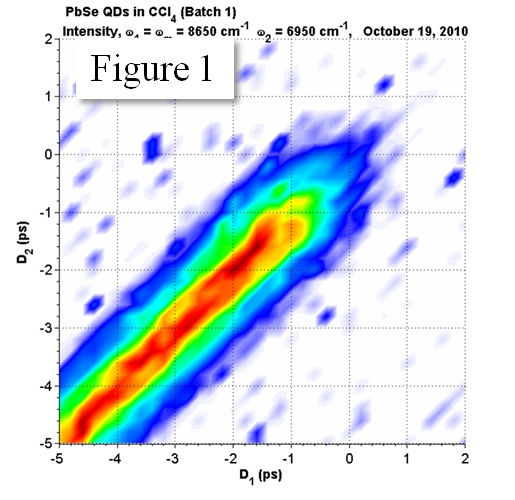
Perhaps the most visible difference between TRIVE and TREE is the nature of the excitations.  Since typical electronic coherences are ~100 times shorter than typical vibrational coherences, a string of resonant interactions can be resonant only for a short window of time, often only over the time of the exitation pulses themselves.  In figure 1, we see time-dependence of TREE signal with w1 and w2 tuned to two different electronic states of PbSe quantum dots.  Unlike vibrational delay scans, signal is only persistent along the population pathways, and the time of which signal last corresponds to the width of our pulses.  The coherences observed here are due mainly to the driving of our laser polarization; dephasing happens so fast that it cannot be observed at times beyond when our laser is actively driving it.  In other words, if the pulses are longer in time than the dynamics of the system, we cannot trace out separate pathways.

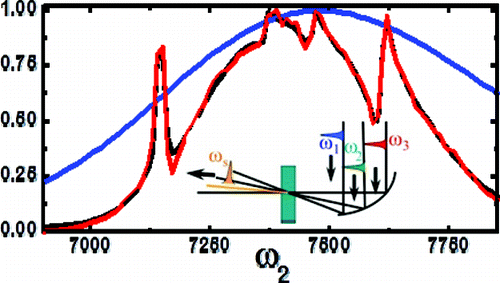
In order to get signal from a particular triply resonant pathway, then, one must sacrifice the luxury of choosing time-ordered pathways, and instead expect several of the pathways to be driven simultaneously.  Figure 2a shows the frequency dependence of a sample that has dephasing times much shorter than the pulse widths.  Even with the added complexity of inhomogeneous broadening, such a cacophony of interactions can be understood through fitting analytic models, as shown in the frequency scan of PbSe quantum dots, and the corresponding fit, in figure 2.

If the number density is large enough, partially resonant signal can also be detected, often from species other than the analyte.  In some studies, Raman transitions from abundant solvent molecules were stimulated to interfere with analyte ouput, as shown in figure 3.  In this way, the solvent can be used as an internal standard, which allows us to make quantitative measurements of the nonlinear susceptability of the analyte.  Additionally, the frequency dependence of this interference can be used to sort out the frequency dependence of real and imaginary parts of the analyte nonlinear susceptability, which can yield system dynamics much faster than the laser pulses themselves.  In the case of figure 3, for instance, dynamics were derived that were much shorter than the actual pulses used to probe the system. 

Current group work is focussed on teasing out the muddled pathways by decreasing the length of our pulses (to ~50 fs) and slowing the dephasing of electronic states through cryogenic cooling.  This will put specral selectivity on the same level as TRIVE, which will allow a multitude of electronic states and dynamics to be resolved.